Research interests

Page en cours de construction

ACTIVITE DE RECHERCHE

Introduction

J’ai eu l’occasion d’effectuer une recherche sur trois thèmes. D’abord en mécanique des fluides sur la dynamique de la vorticité des filaments tourbillons. J’ai réalisé cette recherche à l’occasion de ma thèse [1] sous la direction de J-P. Brancher, de mon DEA, de mon année de 1/2 ATER au LEMTA à Nancy. Puis durant mon postdoc à l’Institut de Mathématique de l’Université de Warwick (UK) avec D. Barkley, j’ai étudié le mouvement de front d’ondes dans des milieux excitables tridimensionnels. Le domaine d’étude est celui de deux équations de réaction-diffusion couplées. Puis lors de mon postdoc à l’IMFT (Toulouse) avec A. Giovannini et P. Brancher, j’ai étudié l’évolution des sillages d’avions à l’aide de méthodes tourbillonnaires qui sont des méthodes numériques Lagrangiennes.

Dans ces recherches, les études effectuées combinent réduction asymptotique et résolution numérique, avec une part plus importante pour l’une ou l’autre suivant le point particulier à traiter. Dans ce qui suit, je présente ces trois thèmes de recherche.

Mouvement des filaments tourbillons en hydrodynamique (Fév. 93-Nov. 98)

Introduction

Le champ de vorticité est le rotationnel du champ de vitesse et celui-ci a un rôle important en hydrodynamique. En effet, dans bon nombre de situations, la vorticité n’est non-nulle que proche de singularités surfaciques ou de courbes. La dynamique de la vorticité dépasse largement son cadre hydrodynamique initial et on retrouve aussi des tourbillons dans d’autres domaines de la physique [2,3,4].

Le champ de vorticité a un rôle important dans le calcul de l’évolution des écoulements incompressibles rotationnels et peu visqueux. Un filament tourbillonest un cas particulier d’écoulement rotationnel pour lequel la vorticité se trouve uniquement dans un tube tridimensionnel dont la ligne centrale est une courbe dite fibre centrale du filament. Très souvent ces filaments sont de faible section (par rapport au rayon de courbure du tube) : on dit que la vorticité est concentrée.

Connaissant le champ de vorticité, le champ de vitesse induit par ce champ est déterminé à un champ de gradient près par la loi de Biot et Savart qui fait intervenir une intégrale sur le domaine de vorticité. Pour un écoulement peu visqueux, on sait qu’à l’ordre principal, le champ de vorticité subit les mêmes déformations que le fluide : on dit que le champ de vorticité est gelé dans le fluide.

Calculer l’écoulement, c’est déterminer l’évolution de cette zone de vorticité qui forme le filament tourbillon, c’est à dire trouver le mouvement de sa fibre centrale. Comme on trouve ces filaments dans les sillages, les couches limites et les écoulements turbulents cite{Moffatt94}, il est donc important de bien connaître leur dynamique.

L’étude des filaments tourbillons a, entre autre, deux utilités importantes. D’une part, elle peut servir au développement des méthodes numériques tourbillonnaires[5,6], qui discrétisent le champ de vorticité de l’écoulement en un grand nombre de filaments tourbillons. Dans ces méthodes, on trouve l’évolution du champ de vorticité (et donc de l’écoulement) en déterminant l’évolution de tous les filaments. D’autre part, des simulations numériques directes d’écoulements turbulents font apparaître bon nombre de filaments tourbillons et il peut être nécessaire de connaître la dynamique de ces filaments pour obtenir une modélisation de la turbulence [7,8], ou pour généraliser en trois dimensions les modélisations de la turbulence 2D par vortex aléatoires [9].

Objectifs

Nous cherchons l’équation du mouvement de la fibre centrale d’un filament tourbillon de faible épaisseur. Le problème a une petite longueurcaractéristique associée à l’épaisseur de l’anneau et une grande longueur associée à son rayon de courbure. En exploitant cette particularité, on fait intervenir un petit paramètre $\epsilon$ qui est le rapport de ces deux longueurs et on extrait de l’équation de Navier Stokes une équation pour la fibre centraledu filament.

Cette équation est une équation aux dérivées partielles du temps et du paramétre sur la fibre centrale. Celle-ci donne les mécanismes de la propagation et sa résolution numérique est infiniment moins lourde que la résolution numérique directe de l’équation de Navier Stokes (cette résolution nécessiterait un maillage important proche de la fibre centrale).

La difficulté de sa dérivation provient du fait que lorsque le filament a une courbure non nulle, le développement selon le petit paramétre est singulier : le filament sans épaisseur a une vitesse infinie ! On a donc une ‘couche limite’ sur une courbe de l’espace qui est l’analogue de la couche limite de Prandtl sur une plaque plane.

Méthodes

Ce problème est multi-échelles et sa résolution utilise les méthodes des perturbations singulières. Pour résoudre la singularité, on utilise la méthode des Développements Asymptotiques Raccordés (DAR). La première différence entre cette couche limite et celle d’une plaque plane est que, ici, la singularité provient essentiellement de la géométrie et non de la viscosité faible. La seconde est qu’au lieu de travailler proche d’une surface, il faut travailler proche d’une courbe. Le travail le plus précis à ce sujet nous a semblé être celui de Callegari et Ting [10] et son complément dans Klein et Ting [11]. Celui-ci est également présenté dans Ting et Klein [12]. Les résultats obtenus par ces auteurs, la démarche entreprise, les hypothèses et les limitations de celle-ci, ainsi que le déroulement de la méthode est de lecture difficile dans ces publications de part le grand nombre de calculs et de notations, ce qui explique que ces résultats semblent être peu ou mal connus de la communauté scientifique française. Apres avoir digéré les différents calculs de cette approche, ainsi que certains intermédiaires de calculs qui n’apparaissent pas dans les publications, il est apparu que dans la littérature, la méthode de développements de l’intégrale de Biot et Savart est souvant obscure. Pour notre part[13], nous avons résolu la singularité dans l’intégrale de Biot et Savart grâce à la méthode des Développements Asymptotiques Raccordés des intégrales singulières [14].

L’aspect multi-échelles singulier de notre problème de filament tourbillon apparaît radialement sous la forme d’une couche limite (DAR), mais aussi axialement sous la forme d’un caractère oscillatoire où apparaît une distinction entre une longueur d’onde de l’ordre de la grande ou de la petite échelle du problème. Ces ondes courtes ont une dynamique rapide qui s’effectue sur un temps court en $t/\epsilon^2$, qui est le temps d’évolution des ondes de Kelvin. Cette seconde singularité s’écrit sous la forme d’une Méthode d’Echelles Multiples (MEM), dont on étudie le comportement moyen “homogénéisé” (ou central) à l’aide d’une étude à une seule échelle de temps $t$ dit temps normal. Une autre échelle de temps rapide (en $t/\epsilon$) mais moins rapide que les ondes de Kelvin est associée à d’autres ondes et intervient lorsque l’ordre principal du champ de vitesse du filament est axisymétrique mais varie axialement[13]. Ces ondes ne seront pas prises en compte dans notre analyse à une échelle de temps. En plus du caractère singulier du développement, une seconde difficulté est liée au fait qu’on étudie une frontière libre, qui est une courbe mobile. Sa résolution nécessite l’utilisation de coordonnées curvilignes locales associées à une courbe tridimensionnelle et de faire un changement de référentiel sur un repère mobile qui se déplace et se déforme comme la courbe.

Le résultat de l’étude asymptotique est une équation aux dérivées partielles pour la courbe centrale. Sa résolution nécessite la réalisation d’un code numérique spécifique, car cette équation n’a que rarement une solution analytique et n’est pas traditionnelle.

Résultats

On a donné un développement général des champs de vitesse du problème dans la région de la couche limite et dans la région extérieure. Cette description permet de préciser les hypothèses simplificatrices qui peuvent être faites par la suite. De plus, on montre comment cette description et ces développements changent avec le choix des grandeurs d’adimensionnalisation.

On a déterminé précisément la limite extérieure de l’intégrale de Biot et Savart par la méthode des Développements Asymptotiques Raccordés d’intégrales [14], puis la limite intérieure [13]. Un exemple d’utilisation de ce développement intérieur de la formule de Biot et Savart a été donné [13] pour un anneau avec variation axiale de son épaisseur. Tous ces calculs asymptotiques d’intégrales et de couche limite ont été implémentés sur calculateur formel afin de pouvoir les réaliser rapidement ainsi que d’aborder des hypothèses de structure d’anneaux tourbillons plus générales. Ceci a permis entre autre d’obtenir une équation d’évolution de la fibre centrale à un ordre supérieur [15] qui rectifie celle de Fukumoto et Miyazaki [16]. On a fermé le système d’équations à cet ordre en donnant également les équations d’évolution du champ des vitesses interieures, qui est couplé avec l’équation d’évolution de la fibre centrale. Fukumoto et Moffatt[17] ont également donné un ordre supérieur mais pour un anneau circulaire.

Nous avons comparé l’équation d’évolution de Callegari et Ting, qui est l’équation d’évolution du filament à l’ordre principal, avec celles obtenues par des méthodes ad hoc de désingularisation[18], ce qui nous a permis de justifier ces méthodes ad hoc en précisant le lien entre la longueur ad hoc de désingularisation et l’épaisseur de l’anneau tourbillon [19,13]. Cette justification n’avait jamais été faite à partir de l’équation de Callegari et Ting. Klein et Knio [5] ont montré que la solution asymptotique de Callegari et Ting permet de préciser le paramétre numérique de désingularisation qui intervient dans le modèle numérique dit du “tube fin”.

Pour un filament droit perturbé par des perturbations dont la longueur d’onde est de l’ordre de la grande longueur caractéristique, on montre [19] que l’équation d’évolution des filaments de Callegari et Ting se simplifie différemment selon l’amplitude de la perturbation et selon que l’on a un filament ultra-fin, pour lequel le logarithme de l’épaisseurréduite du corps est grand, ou un filament fin, pour lequel le logarithme de l’épaisseur réduite est considéré de l’ordre de 1. Suivant o`u l’on se trouve dans un plan formé par ces deux paramétres : amplitude et épaisseur; on trouve alors soit l’équation d’induction locale, soit une équation linéaire, soit l’équation du régime de Klein et Majda [20].

On a écrit un code numérique en fortran qui résoud l’équation non-linéaire d’évolution de la courbe centrale. Il nous permet d’étudier l’évolution de un ou plusieurs anneaux tourbillons. L’équation à résoudre est une équation intégrodifférentielle pour un vecteur de l’espace avec une dérivée partielle temporelle et une dérivée partielle spatiale. On a utilisé un schéma d’Euler implicite en temps, une différence finie spatiale ainsi qu’une méthode de trapèzes pour le terme intégral.

L’étude de l’évolution linéaire d’un anneau circulaire perturbé a été effectué à l’aide de l’équation de Callegari et Ting, d’une part au moyen d’une étude analytique en modes normaux qui aboutit à une expression analytique de la période d’oscillation de chaque mode, mais également au moyen du code numérique non linéaire en faisant des simulations numériques de perturbations de petite amplitude pour chaque mode.

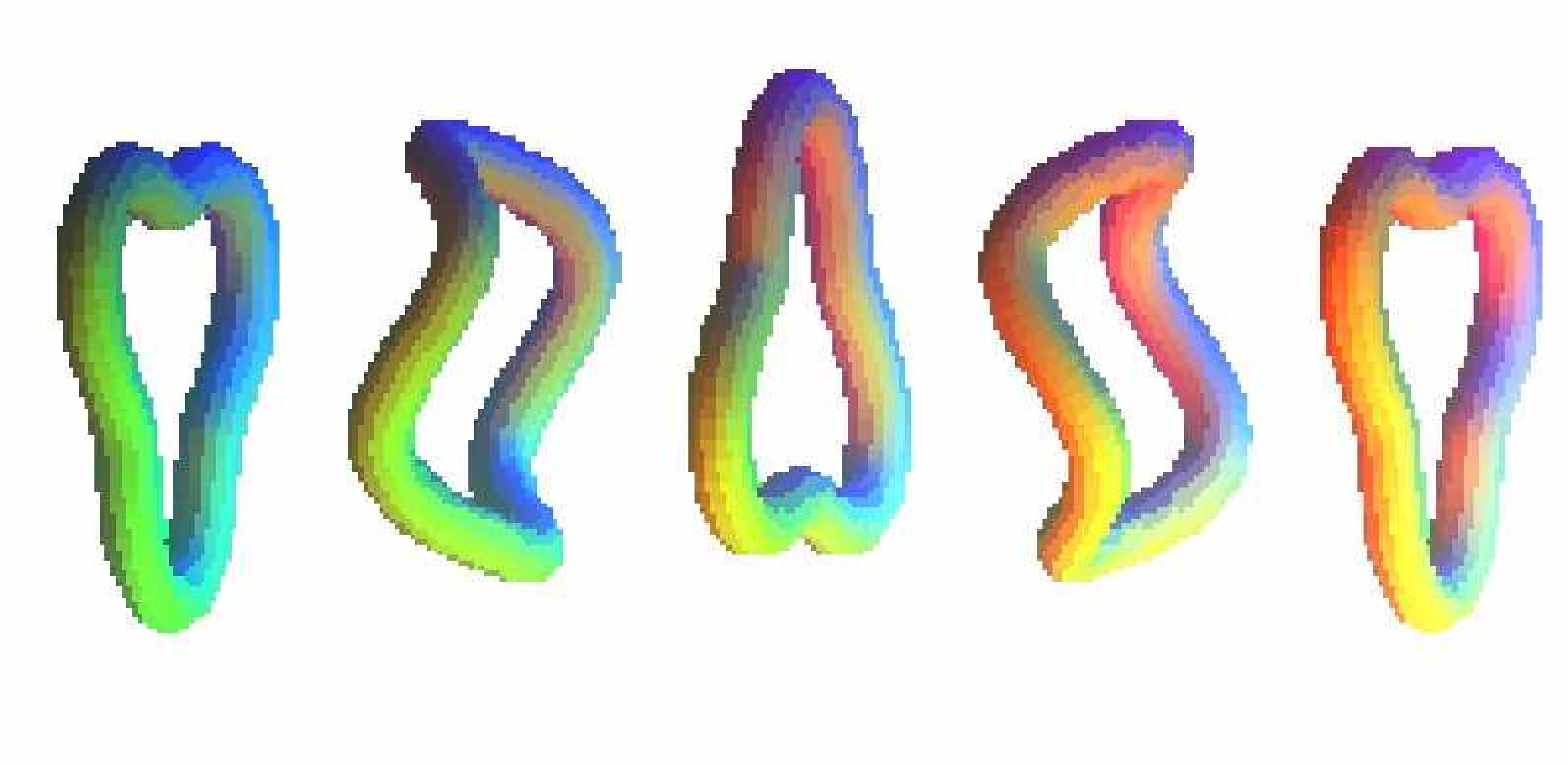
L’étude de stabilité linéaire de ce problème avait été effectuée par Widnall et Sullivan [21], mais ces auteurs n’avaient ni donné d’expression analytique pour la période d’oscillation, ni comparé ces periodes à des résultats de simulations numériques. Les résutats numériques sont en bon accord avec l’étude linéaire en modes normaux, et ceci également pour un anneau visqueux [22].

Perspectives

Différentes perspectives d’extension ou d’utilisation de ce travail ont été mises en évidence, comme l’étude de l’Hélicité (invariant topologique) [23,24] de deux anneaux enlacés ; l’étude d’un filament tourbillon avec une structure qui dépend d’une abscisse sur le filament [25,26], qui est non axisymétrique [27] ou qui peut avoir des petites longueurs d’ondes ; l’étude de l’éclatement tourbillonnaire [28]; l’étude d’une répartition linéique de dipôles sur une courbe [29]; les méthodes numériques tourbillonnaires [30]; ou l’étude de la turbulence [27,8,17].

Travail amorcé

Un système d’équations d’évolution d’un anneau tourbillon de faible épaisseur avec son ordre principal axisymétrique, mais variant selon l’abscisse de la courbe centrale, a été dérivé asymptotiquement à partir des équations de Navier-Stokes [13,31] par une étude à deux échelles de temps. Ce sytème quasi-hyperbolique n’avait jamais été extrait asymptotiquement même si des systèmes modèles ont été proposés [25,26] puis étudiés numériquement. L’évolution des ondes de petites amplitudes a été réalisée par une étude de stabilité linéaire que ce soit pour un coeur gaussien ou de Rankine[31]. Des simulations numériques des équations non linéarisées montrent la formation de chocs en temps fini qui correspondent à la formation d’un éclatement tourbillonnaire sur ces filaments[31,32,33]. La dynamique des bulles tourbillons toriques a été généralisée à des bulles de forme quelconque (i.e.,non circulaires) et avec un coeur non-potentiel (à suivre ...) [31].

Mots clefs

Champ de vorticité, filament et anneau tourbillon, frontière libre, EDPs, développements asymptotiques, intégrales singulières, changement de référentiel, stabilité, calcul formel, simulation numérique, Runge-Kutta, différences finies.

Mouvement de front d’onde dans les milieux excitables (Nov.98-Mars 00)

Introduction

Les systèmes qui peuvent être modélisés par des équations de réaction-diffusion font apparaître parfois un comportement qui est dit excitable. Ces systèmes ont alors un état d’équilibre stable vis à vis de perturbations. Cependant si l’intensité des perturbations dépasse un certain seuil, le système change rapidement d’état et reste dans cet état un certain temps avant de revenir rapidement à son état initial. Le couplage de cet état excitable (du à la forme non-linéaire des termes réactifs) avec la diffusion fait que des ondes peuvent se propager dans le milieu. On observe ces ondes dans bon nombre de systèmes réactifs et biologiques. Un exemple connu d’onde d’un système excitable est l’onde d’activité électrique qui se propage sans se dégrader le long de la membrane des axones du système nerveux. Cette onde a un rôle important sur les perturbations des périodes des battements cardiaques.

En deux dimensions, ces ondes correspondent à la propagation d’un front d’onde et on observe la formation de structures sous la forme d’un front spirale qui tourne autour d’un point fixe. Lorsque les paramètres du milieu sont fixés, cette onde tourne à une fréquence précise. Cet aspect de rotation autour d’un point fixe fait que l’on appelle parfois cette structure “un vortex”. En trois dimensions, le point central devient une courbe et l’onde spirale devient un rouleau spirale qui s’enroule autour de cette courbe, qui est appelée filament tourbillon (Fig. 3).

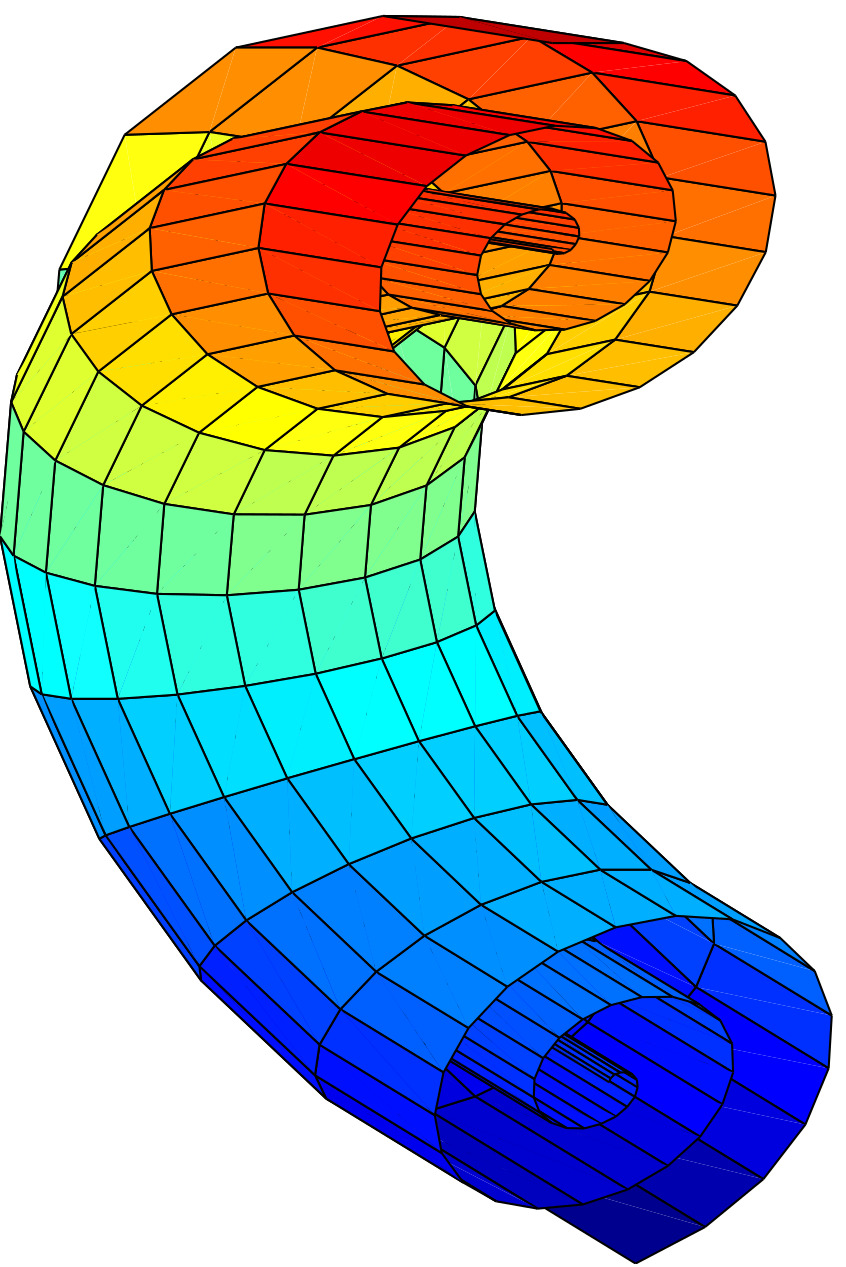
Les fronts d’ondes sont donc des surfaces semi-infinies qui s’enroulent pour former une nappe spirale qui tourne autour du filament central. Dans une coupe plane perpendiculaire au filament, on observe une onde spirale. Lorsque la phase de cette spirale varie le long du filament, la nappe spirale est vrillée et on parle du twist du filament.

Un milieu excitable peut être modélisé par la classe générale suivante d’équations de reaction-diffusion :

\begin{eqnarray} \begin{split} \epsilon^2\partial{u}/\partial{t}&=&\epsilon^2\nabla^2u+f(u,v),\\ \partial{v}/\partial{t}&=&\delta^3\nabla^2v+\epsilon g(u,v), \end{split} \label{eq:rd} \end{eqnarray}

où $\epsilon\ll1$, et $f$ et $g$ sont les termes réactifs avec $f(u,v)=0$ de forme cubique. Ici, $\delta$ est un coefficient de diffusion de la concentration $v$. L’excitabilité de la solution de ce système provient de la petitesse de $\epsilon$. Une première approche pour étudier les solutions de ce système \eqref{eq:rd} est sa simulation numérique directe. En deux dimensions le code EZ-spiral développé par D. Barkley [34] résoud le système \eqref{eq:rd} sur une grille fixe et avec des coordonnées cartésiennes. Les solutions stationnaires bidimensionnelles (ou se ramenant à un problème bidimensionnel) vérifient le système suivant

\begin{eqnarray} \begin{split} -\omega \epsilon^2\partial{u}/\partial{\varphi}&=&\epsilon^2\Delta^2u+f(u,v), \\
-\omega \partial{v}/\partial{\varphi}&=&\delta^3\Delta^2v+\epsilon g(u,v), \end{split} \label{systeme2s} \end{eqnarray}

qui est écrit avec des coordonnées polaires. On a un problème de recherche de la valeur propre $\omega$. La résolution numérique du système \eqref{systeme2s} et l’étude numérique de la stabilité linéaire de la solution a été étudié [35]. Le code EZ-scroll développé par D. Barkley généralise le code EZ-spiral à la dimension trois. En trois dimensions, les simulations numériques [36,37,38,39,40,41,42] et les expériences montrent que le filament central ne reste pas immobile : contrairement au filament droit, il se met à bouger tout doucement. Même si ce phénomène est une réalité expérimentale et numérique, il est encore mal compris.

Une autre approche pour obtenir la solution des équations \eqref{eq:rd} est d’exploiter la petitesse de $\epsilon$ en employant des méthodes de perturbations singulières afin d’obtenir une solution asymptotique à petit $\epsilon$. La solution asymptotique de \eqref{eq:rd} n’est pas régulière spatialement et le développement de la solution doit être donné dans trois régions : deux couches limites et la région complémentaire, appelée région extérieure. La première couche limite se trouve proche du front (zone interfaciale) et la seconde au centre de rotation (zone du corps). Ces deux zones se raccordent asymptotiquement avec la zone extérieure. Cette approche a été réalisée avec succés en 2-d, où une solution stationnaire (rotation constante) a été trouvée [43,44,45,46,47] pour $\delta\ll\epsilon$ et $\epsilon\ll\delta\ll1$. L’étude de leur stabilité a également été faite [47]. La solution est composée de la solution extérieure : champ de concentrations $u$ et $v$ et forme de l’interface, ainsi que du corps : champ de concentrations $u$ et $v$. Peu d’études analytiques ont été entreprises en 3-d [48,49,50,51,52,53,54,55]. Les études [49,50,53,54,55] sont des approches phénoménologiques. Le cas 3-d a été aussi étudié par des méthodes de perturbations [48,51,52], mais d’une façon différente du cas 2-d et une équation d’évolution du filament a été avancée.

Objectifs

Les résultats précédents ont quelques limitations importantes :

-L’équation du mouvement obtenue est donnée uniquement pour un filament presque droit (faible courbure) sans utiliser l’avantage de la petitesse du paramètre $\epsilon$ des équations \eqref{eq:rd}).
-La valeur des coefficients dans cette équation du mouvement n’est pas donnée explicitement en fonction des paramètres de l’équation de réaction-diffusion \eqref{eq:rd}. -Il n’y a pas de relation entre les équations écrites en 3-d et les solutions asymptotiques ($\epsilon\ll 1$) trouvées en 2-d. Ainsi, comme cas particulier des équations écrites en 3-d, on ne retrouve pas les solutions trouvées en 2-d. -En 2-d, il n’y a pas de comparaison quantitative entre résultats asymptotiques et numériques.

Le mérite des travaux précédents en 3-d est que ces résultats on été avancés avant qu’une solution asymptotique satisfaisante du cas 2-d ait été obtenue. Cependant comme la solution 2-d est désormais assez bien connue [43,44,45,46,47], il est temps de résoudre le cas 3-d par une approche asymptotique ($\epsilon\ll 1$) qui généralise les résultats asymptotiques 2-d. Il est également intéressant d’avoir une confrontation entre résultats numériques et asymptotiques.

Méthodes et Résultats

Nous avons donné une description de la géométrie 3-d qui généralise celle faite en 2-d tout en la contenant. A l’aide de cette géométrie des surfaces, des courbes et des points de l’espace 3-d, nous avons écrit les équations \eqref{eq:rd} sur les coordonnées liées à ces géométries [56]. Les échelles asymptotiques ($\epsilon\ll 1$) solutions du problème ont alors été déterminées, ce qui a aboutit à l’écriture du système d’équations sous la forme \eqref{eq:rd}. L’écriture du système sous cette forme n’est en fait pas innocente et contient déjà une partie non triviale de la réponse au problème. Cette écriture est également utile pour les simulations numériques directes à $\epsilon$ petit car les champs, les vitesses et les distances restent alors de l’ordre de 1. En remplaçant les développements asymptotiques dans \eqref{eq:rd} et en effectuant le raccord entre la solution dans l’interface et dans la zone extérieure, on a extrait l’ordre principal des équations. C’est un système couplé d’équations entre la concentration de $v$ et l’interface. La solution asymptotique de la couche limite au niveau du front surfacique a été donnée à l’ordre principal, en montrant que la solution de cette couche limite se raccorde bien asymptotiquement (DAR) avec la solution du problème extérieur. Il a été montré que la règle de raccord asymptotique donne la même équation d’évolution du front d’onde que l’alternative de Fredholm généralement utilisée. Cependant, de façon naturelle, il est plus convenable d’utiliser la règle de raccord asympotique dans une situation de couche limite et c’est la seule qui peut être appliquée si l’on veut trouver l’ordre supérieur.

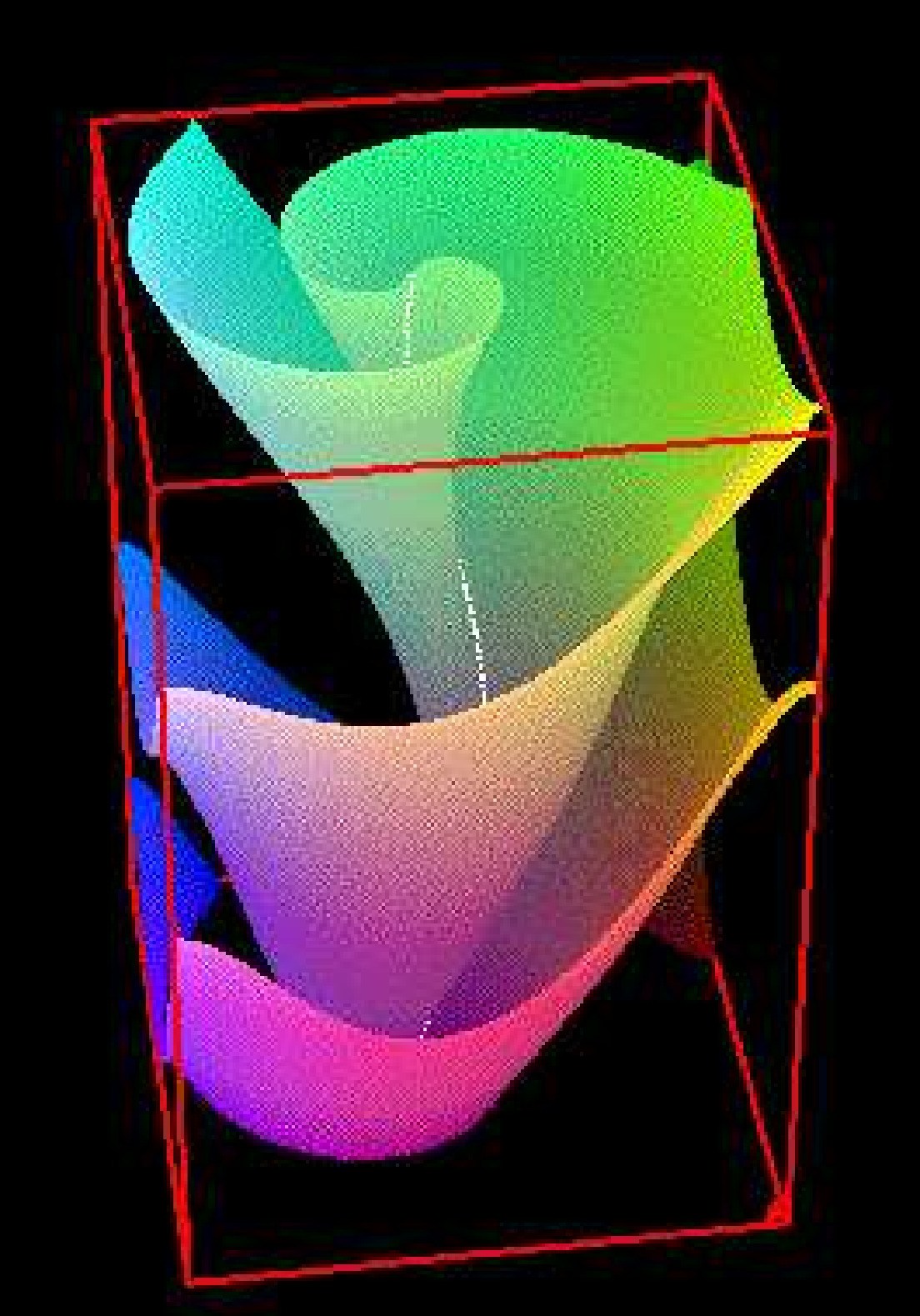
Pour de petites valeurs du paramètre $\epsilon$, nous avons fait des simulations directes avec EZ-scroll d’un filament droit twisté (Fig. 4) et d’un filament en forme d’hélice, ainsi que des simulations directes d’évolution de spirales avec EZ-spiral. Un filament droit twisté de twist constant est une solution stationnaire de \eqref{eq:rd}. Pour un tel filament, on retrouve[56] les résultats analytiques de Bernoff [43] à partir de l’ordre principal des équations que l’on a trouvées.

Un code spectral a été écrit pour résoudre le problème aux valeurs propres bidimensionnel \eqref{systeme2s} (généralisé à un twist non nul) sur des coordonnées polaires. Les fréquences de rotation $\omega$ obtenues par ces simulations numériques directes sont en accord avec les résultats analytiques précédents. Le résultat ainsi obtenu [57] donne la première comparaison quantitative entre résultat asymptotique et résultat numérique pour ce problème. En traçant l’évolution de $\omega$ avec $\epsilon$, ces simulations donnent également la correction de $\omega$ due à l’ordre supérieur. Pour la spirale 2-d stationnaire, nous avons fait une description asymptotique de tous les champs à l’ordre principal et au premier ordre dans la région de l’interface et la région extérieure [58,57]. Le résultat obtenu pour le premier ordre permet d’avoir toute une zone de recouvrement en $\epsilon$ entre le résultat du à la simulation directe et le résultat asymptotique [57].

En 3-d, l’ordre principal et le premier ordre des équations dans le corps ont été donnés [56]. Sous l’hypothèse de l’immobilité du filament, une singularité devrait apparaître dans ces équations lors du raccord entre les différentes régions asymptotiques. La détermination de cette singularité devrait conduire à l’ordre de grandeur en puissances de $\epsilon$ de la vitesse de déplacement du filament ainsi qu’à l’équation d’évolution de ce filament.

Perspectives

En 2-d pour la solution stationnaire, la comparaison entre les champs dans le corps obtenus par la méthode de perturbations et par les simulations numériques directes à petit $\epsilon$ n’a jamais été effectuée. Le premier ordre des équations dans le corps n’a jamais été résolu numériquement malgré que cet ordre intervient dans l’étude linéaire de stabilité du corps [47], ce qui laisse quelques doutes sur cette étude de stabilité. Pour la solution instationnaire sans diffusion de la concentration $v$ ($\delta=0$), il n’y a pas de résolution numérique des équations d’interfaces à l’ordre principal, ni de comparaison avec les résultats que peut donner le code EZ-spiral instationnaire à petit $\epsilon$. L’équation du mouvement du filament tourbillon n’a encore pas été déduite des équations sous-jacentes même si l’on a fait un grand pas dans cette direction[56]. Cette connaissance serait importante à avoir vis - à - vis des implications biologiques pour lesquelles le système de réaction-diffusion régit l’évolution du potentiel électrique de contrôle des battements du muscle cardiaque.

Travail amorcé

En 3-d, les équations à l’ordre principal et au premier ordre deviennent instationnaires. Des simulations numériques 3-d sont réalisées dans la limite des petits $\epsilon$ afin de déterminer l’ordre de la vitesse d’évolution lente des filaments et ainsi sélectionner les développements asymptotiques à prendre dans les approches de perturbations et d’obtenir une équation théorique pour le mouvement du filament (à suivre ...).

Mots clefs

équations de Réaction-diffusion, nappe spirale, milieu excitable, front d’onde, développements asymptotiques, changement de référentiel, frontière libre, surfaces et courbes mobiles, stabilité, simulations numériques directes, différences finies, méthodes spectrales, perturbations cardiaques, tachycardie.

Simulation Lagrangienne de sillage d’avion (Mars 00-Mars 02)

Introduction

La construction du gros porteur A380 par Airbus demande un regain d’intérêt pour le comportement des sillages d’avion. Les constructeurs veulent augmenter le trafic des aéroports dejà saturés en utilisant un avion à deux étages. Il ne faut pas que la grande taille de l’avion crée un sillage plus persistant que les précédants car ceci diminuerait la fréquence de décollage des avions, qui attendent que le sillage de l’avion précédent ne soit plus dangereux pour décoller. Les autorités des aéroports demandent au constructeur que son avion satisfasse aux fréquences et aux marges de sécurités actuelles et lui demande de le lui certifier.

Objectifs

Dans ce cadre, le contrat européen C-Wake a été mis en place pour que industriels et universitaires s’unissent afin d’apporter les éléments de réponse nécessaires: des études théoriques, numériques et des expériences de laboratoire et de grandeur nature sont entreprises. J’interviens dans ces études dans le cadre des simulations numériques simplifées. On veut faire des études paramètriques approchées afin de situer les paramètres qui réduisent la persistance du sillage. D’autres partenaires feront alors des études numériques plus coûteuses dans les configurations les plus prometteuses qui auront été ainsi déterminées de façon approchée.

Méthodes

Nous utilisons des méthodes numériques Lagrangiennes dites méthodes de tourbillons. Les équations du fluide sont écrites en vorticité, c’est à dire que l’on utilise l’équation de la vorticité et le noyaux de Biot et Savart qui donne le champ de vitesse induit par un champ de vorticité connu. L’avantage de ces méthodes est que l’on ne discrétise numériquement que la zone de vorticité qui n’occupe qu’une petite partie de l’écoulement: typiquement les deux tourbillons de bout d’aile. Ces méthodes Lagrangiennes sont des méthodes particulaires: on déplace une particule de vorticité par le champ de vitesse, on l’étire et la réoriente par le champ de déformation, et on la fait diffuser. Ces méthodes ont l’avantage de ne pas avoir de diffusion numérique. Une section du filament tourbillon doit contenir un nombre suffisant de particules pour assurer la convergence de la méthode numérique. Nous possédons un code[59] de méthodes de tourbillons 3D, mais comme l’utilisation de celui-ci revient à faire une simulation numérique directe 3D, ce qui est très coûteux, il ne répond pas exactement à notre demande de simulation simplifiée.

L’ulilisation de la méthode numérique précédente en ne prenant qu’une particule par section de filament est séduisante car elle diminue les temps des simulations, mais elle donne des résultats erronés comme l’ont montré Klein et Knio [5] par comparaison avec des résultats asymptotiques pour des filaments de faible épaisseur. Cette même comparaison a permis à Klein et Knio [5] de préciser comment cette méthode pouvait être utilisée en corrigeant son résultat de façon théorique. La méthode a été modifiée récemment [60] afin de n’être plus raide (nombre de particules importantes le long du filament) comme elle l’était auparavant.

Résultats

J’ai implémenté la méthode de Klein et Knio [60] de filaments de faible épaisseur dans un code en C (EZ-vortex) avec des sorties graphiques 3D qui utilisent la bibliothèque graphique OpenGL. Les dérivées spatiales sont évaluées spectralement et une méthode d’Adams-Bashforth (second ordre) est utilisée pour l’avancement en temps. Le code permet de simuler des filaments fermés ou ouverts. Il a été validé par comparaison avec des résultats de stabilités linéaires.

Le code EZ-vortex est documenté et est d’utilisation facile: suite à son utilisation pour le contrat européen et les publications associées, il sera mis à disposition sur le web dans un intérêt pédagogique (enseignement en vorticité) et de recherche. Cette attitude a été adoptée par D. Barkley pour ses codes EZ-spiral et EZ-scroll sur les milieux excitables.

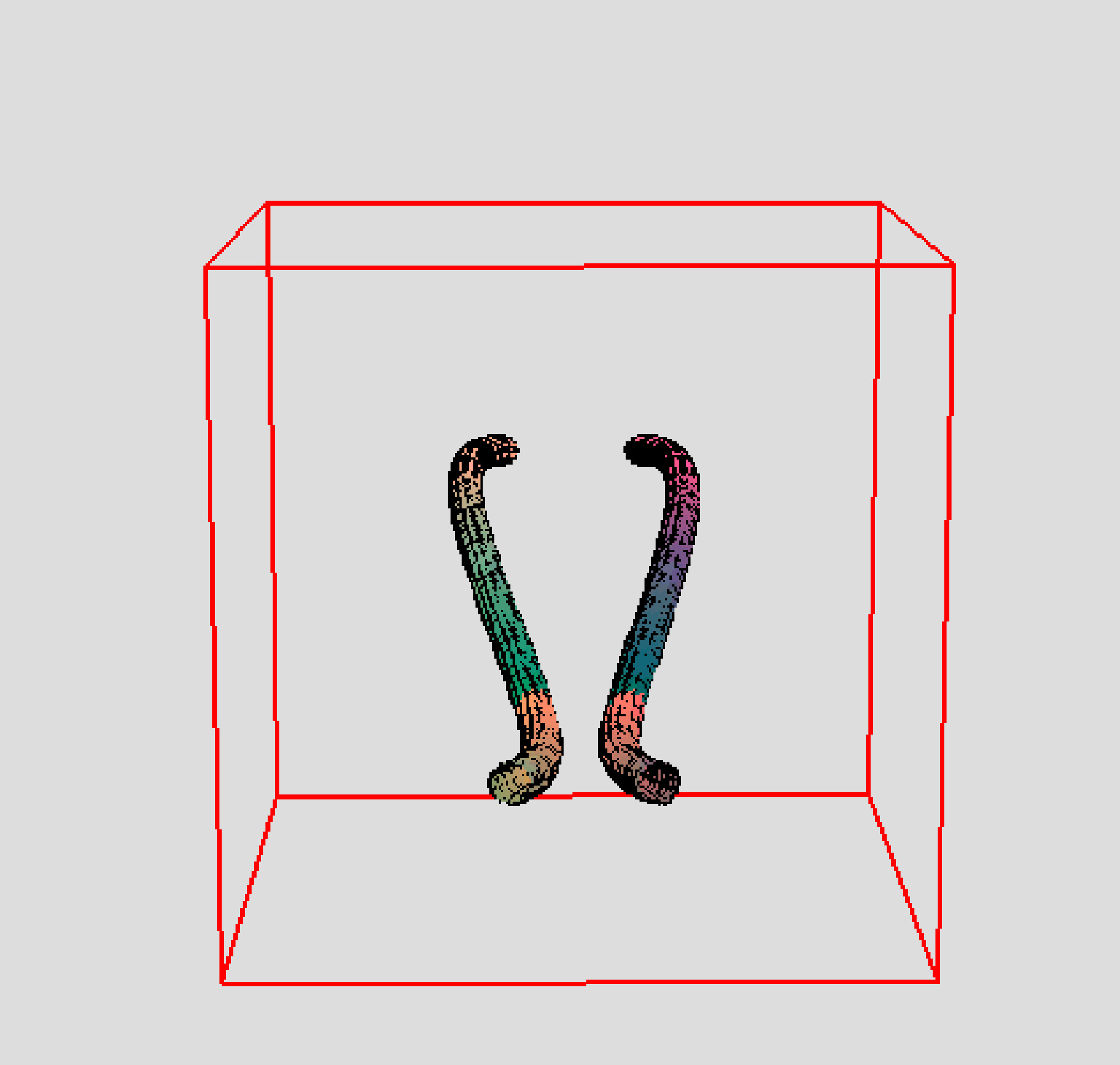
Perspectives

La limitation des méthodes filaments de faible épaisseur est de n’être correcte que dans la limite asymptotique des faibles épaisseurs. Cette méthode numérique pourrait être étendue à des filaments plus épais en utilisant la première correction asymptotique de l’équation d’évolution[15]. La correction à apporter à la méthode numérique pour qu’elle soit correcte pour des filaments plus épais est à l’étude et sera ensuite implémentée dans le code.

La seconde limitation de cette méthode et de ne pas pouvoir faire de reconnection des filaments. Un modèle simplifié de reconnection qui serait une alternative à la simulation directe n’est malheureusement pas encore connu.

Mots clefs

Sillage, tourbillons de bout d’aile, méthodes tourbilonnaires.

1. [1]D. Margerit, Mouvement et dynamique des filaments et des anneaux tourbillons de faible épaisseur, PhD thesis, Institut National Polytechnique de Lorraine, 1997.
2. [2]S.J. Chapman, A mean-field model of superconducting vortices in three dimensions, SIAM J. Appl. Math. 55 (1995) 1259‑1274.
3. [3]A.Y.K. Chui, H.K. Moffatt, The energy and helicity of knotted magnetic flux tubes, Proc. R. Soc. London A. 451 (1995) 609‑629.
4. [4]K.W. Shwartz, Three-dimensional vortex dynamics in superfluid H4:Homogeneous superfluid turbulence, Phys. Rev. B. 38 (1988) 2398‑2417.
5. [5]R. Klein, O.M. Knio, L. Ting, Representation of Core dynamics in slender vortex filament simulations, Phys. Fluids. 8 (1996) 2415-.
6. [6]A. Leonard, Computing three-dimensional incompressible flows with vortex elements, Ann. Rev. Fluid Mech. 17 (1985) 523‑559.
7. [7]S.L. Dizès, M. Rossi, H.K. Moffatt, On the three-dimensionnal instability of elliptical vortex subjet to stretching, Phys. Fluids. 8 (1996).
8. [8]H.K. Moffatt, S. Kida, K. Ohkitani, Stretched vortices-the sinews of turbulence;large-Reynolds-number asymptotics, J. Fluid Mech. 259 (1994) 241‑264.
9. [9]A.J. Chorin, Vorticity and turbulence, Springer, 1994.
10. [10]A.J. Callegari, L. Ting, Motion of a curved vortex filament with decaying vortical core and axial velocity, SIAM J. Appl. Math. 35 (1978) 148‑175.
11. [11]R. Klein, L. Ting, Vortex filaments with axial core structure variation, Appl.Math.Lett. 5 (1992) 99‑103.
12. [12]L. Ting, R. Klein, Viscous Vortical Flows (Monograph), Lecture Notes in Physics, 1991.
13. [13]D. Margerit, J.-P. Brancher, Asymptotic Expansions of the Biot-Savart law for a slender vortex with core variation, Journal of Engineering Mathematics. (2001).
14. [14]C. François, Les méthodes de perturbation en mécanique, ENSTA, Paris, 1981.
15. [15]D. Margerit, The complete first order expansion of a slender vortex ring, in: E. Krause, K. Gersten (Éd.), IUTAM Symposium on Dynamics of Slender Vortices, Kluwer academic publishers, Aachen, 31 Aug.-3 Sep. 1997: p. 45‑54.
16. [16]Y. Fukumoto, T. Miyazaki, Three dimensional distortions of a vortex filament with axial velocity, J. Fluid Mech. 222 (1991) 369‑416.
17. [17]Y. Fukumoto, H.K. Moffatt, Motion and expansion of a viscous vortex ring. Part1. A higher-order asymptotic formula for the velocity, J. Fluid Mech. 417 (2000) 1‑45.
18. [18]S.C. Crow, Stability theory for a pair of trailing vortices, AIAA J. 8 (1970) 2172‑2179.
19. [19]D. Margerit, J.-P. Brancher, The different equations of motion of the central line of a slender Vortex Filament and their use to the study of perturbed Vortices, Esaim (European Series in Applied and Industrial Mathematic). (1999) 1‑10.
20. [20]R. Klein, A.J. Majda, Self-stretching of a perturbed vortex filament \symbol73: the asymptotic equation for derivations from a straight line, Physica D. 49 (1991) 323‑352.
21. [21]S.E. Widnall, J.P. Sullivan, On the stability of vortex rings, Proc. R. Soc. London A. 332 (1973) 335‑353.
22. [22]D. Margerit, J.-P. Brancher, Motion and oscillations of a circular perturbed vortex ring, C. R. Acad. Sci. Paris, Série II b. 328 (2000) 1‑6.
23. [23]H.K. Moffatt, The degree of knottedness of tangled vortex lines, J. Fluid Mech. 35 (1969) 117‑129.
24. [24]H.K. Moffatt, L.R. Ricca, Helicity and the Călugăreanu invariant, Proc. R. Soc. Lond. A. 439 (1992) 411‑429.
25. [25]T.S. Lundgren, W.T. Ashurts, Area-varying waves on curved vortex tubes with application to vortex breakdown, J. Fluid Mech. 200 (1989) 283‑307.
26. [26]J.S. Marshall, A general theory of curved vortices with circular cross-section and variable core area, J. Fluid Mech. 229 (1991) 311‑338.
27. [27]T.S. Lundgren, Strained spiral vortex model for turbulent fine structure, Phys. Fluids. 25 (1982).
28. [28]S. Leibovich, S.N. Brown, Y. Patel, Bending waves on inviscid columnar vortices, J. Fluid Mech. 173 (1986) 595‑624.
29. [29]L. Ting, F. Bauer, Viscous Vortices in two- and three-Dimensional Space, Computer Fluids. 22 (1993) 565‑588.
30. [30]R. Klein, O.M. Knio, Asymptotic vorticity structure and numerical simulation of slender vortex filaments, J. Fluid Mech. 284 (1995) 257‑321.
31. [31]D. Margerit, Axial core-variation of axisymmetric shape on a curved slender vortex filament with a Batchelor, Rankine, or bubble core, (s. d.).
32. [32]M.O. Souza, S.J. Cowley, On wave phenomena in vortex breakdown, (s. d.).
33. [33]M.O. Souza, Instabilities of rotating and unsteady flows, PhD thesis, Darwin College, University of Cambridge, 1998.
34. [34]D. Barkley, A model for fast computer simulation of waves in excitable media, Physica D. 49 (1991) 61‑70.
35. [35]D. Barkley, Spiral Meandering, Kluwer, 1995.
36. [36]M. Dowle, R.M. Mantel, D. Barkley, Fast simulations of waves in three-dimensional excitable media, Int. J. of Bifurcation and Chaos. 7 (1997) 2529‑2545.
37. [37]A.T. Winfree, Stable Particle-Like Solutions to the Nonlinear Wave Equations of Three-Dimensional Excitable Media, SIAM Review. 32 (1990) 1‑53.
38. [38]A.T. Winfree, Lingering mysteries about organizing centers in the beluzov-zhabotinsky medium and its oregonator model., in: R. Kapral, K. Showalter (Éd.), Chemical Waves and Patterns, Kluwer, 1995: p. 3‑5.
39. [39]A.T. Winfree, Persistent tangles of vortex rings in excitable media, Physica. D. 84 (1995) 126‑147.
40. [40]A.T. Winfree, S.H. Strogatz, Singular filaments organize chemical waves in three dimensions: II. Twisted waves, Physica D. 9 (1983) 65‑80.
41. [41]A.T. Winfree, S.H. Strogatz, Singular filaments organize chemical waves in three dimensions: III. Knotted waves, Physica D. 9 (1983) 333‑345.
42. [42]A.T. Winfree, S.H. Strogatz, Singular filaments organize chemical waves in three dimensions: IV. Wave taxonomy, Physica D. 13 (1984) 221‑233.
43. [43]A.J. Bernoff, Spiral wave solution for reaction-diffusion equations in fast reaction/slow diffusion limit, Physica D. 53 (1991) 125‑150.
44. [44]A. Karma, Scaling Regime of Spiral Wave Propagation in Single-Diffusive Media, Physical Review Letters. 68 (1992) 397‑400.
45. [45]D.A. Kessler, H. Levine, W. Reynolds, Spiral-core in singly diffusive excitable media, Physical Review Letters. 68 (1992) 401‑404.
46. [46]D.A. Kessler, H. Levine, W. Reynolds, Spiral-core meandering in excitable media, Physical Review A. 46 (1992) 5264‑5267.
47. [47]D.A. Kessler, H. Levine, W.N. Reynolds, Theory of spiral core in excitable media, Physica D. 70 (1994) 115‑139.
48. [48]V.N. Biktashev, A.V. Holden, H. Zhang, Tension of organizing filaments of scroll waves, Phil. Trans. R. Soc. Lond. A. 347 (1994) 611‑630.
49. [49]P.K. Brazhnik, V.A. Davydov, V.S. Zykov, A.S. Mikhailov, Vortex rings in excitable media, Sov.Phys. JETP. 66 (1987) 984‑990.
50. [50]R.C. Brower, D.A. Kessler, J. Koplik, H. Levine, Geometrical models of interface evolution, Physical Review A. 29 (1984) 1335‑1342.
51. [51]J.P. Keener, The dynamics of three dimensional scroll waves in excitable media, Physica D. 31 (1988) 269‑276.
52. [52]J.P. Keener, J.J. Tyson, The Dynamics of Scroll Waves in Excitable Media, SIAM Review. 34 (1992) 1‑39.
53. [53]A.S. Mikhailov, V.S. Zykov, Kinematical theory of spiral waves in excitable media: Comparison with numerical simulations, Physica D. 52 (1991) 379‑397.
54. [54]H. Yamada, K. Nozaki, Dynamics of wave fronts in excitable media, Physica D. 64 (1993) 153‑162.
55. [55]H. Yamada, K. Nozaki, Dynamics of untwisted scroll rings in excitable media, Journal of the physical society of Japan. 63 (1994) 379‑382.
56. [56]D. Margerit, D. Barkley, Large-Excitability Asymptotics for Scroll Waves in Three-Dimensional Excitable Media, (s. d.).
57. [57]D. Margerit, D. Barkley, Selection of twisted scroll waves in three-dimensional excitable media, Physical Review Letter. 86 (2001) 175‑178.
58. [58]D. Margerit, D. Barkley, First orders of the concentration fields, the interface shape and the frequency of a stationary straight scroll filament with twist, (s. d.).
59. [59]G.-H. Cottet, P. Koumoutsakos, Vortex methods: theory and practice, Cambridge University Press, Cambridge, 2000.
60. [60]O.M. Knio, R. Klein, Improved thin-tube models for slender vortex simulations, J. Comput. Phys. 163 (2000) 68‑82.